今回は、
「正四・正八・正二十面体」
の話ではありません。
前回の、
「正三角形6個のみで構成された平行四辺形BCIR」
という展開図を組み立てた立体についての補足です。
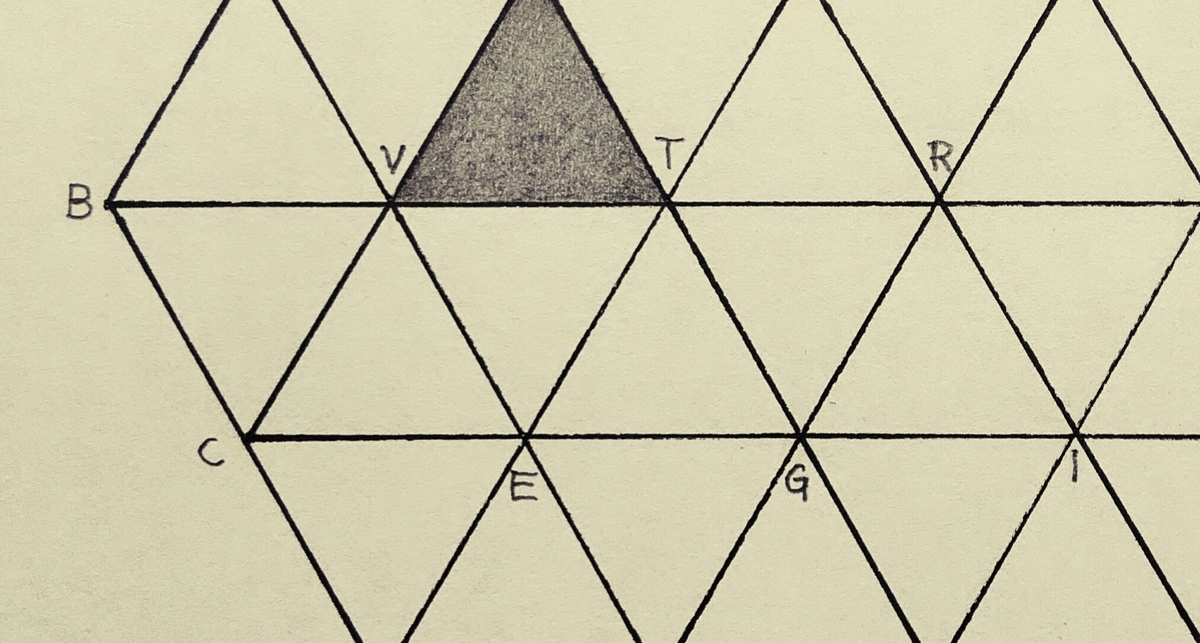
展開図からも明らかなように、
「合同な正多角形のみで構成された多面体」
ですが、“正多面体”ではありません。
なぜなら、
「各頂点に集まる面の数が同じではない」
からですね。
(※同様の多面体は他にもあります。)
この立体には、
“外接球(全ての頂点を通る)”
や、
“平行な面”
は存在しませんが、
“内接球(全ての面に接する)”
は存在しますね。
この立体が、
「2つの正四面体が合体した立体」
であることから上記をイメージできればOKです。
(“内接球の中心”もイメージできるようにしましょう。)
中3生ならば秋頃には、この“内接球の半径”も求められるようになっているはずです。
※なお、この立体の見取り図を次のように描かれることで、混乱してしまうことのないようにしましょう。
