「柱体・錐体である多面体」
の体積ならば、簡単に求められる場合もありますね。
しかし入試問題では、柱体・錐体であっても、
「底面に対する高さ」
が求めにくい場合が多くなります。
ましてや、
「柱体・錐体ではない多面体」
であるならば、その体積を求めるには、何らかの工夫が必要になってきます。
そのための練習をしておきましょう。
(※高学年の小学生ならば解けるレベルにしてあります。)
【問題】
1辺12の立方体ABCD-EFGHがある。
辺AE,EF,BC上の点をそれぞれI,J,Kとする。
AI=FJ=CK=4とするとき、次の問いに答えよ。
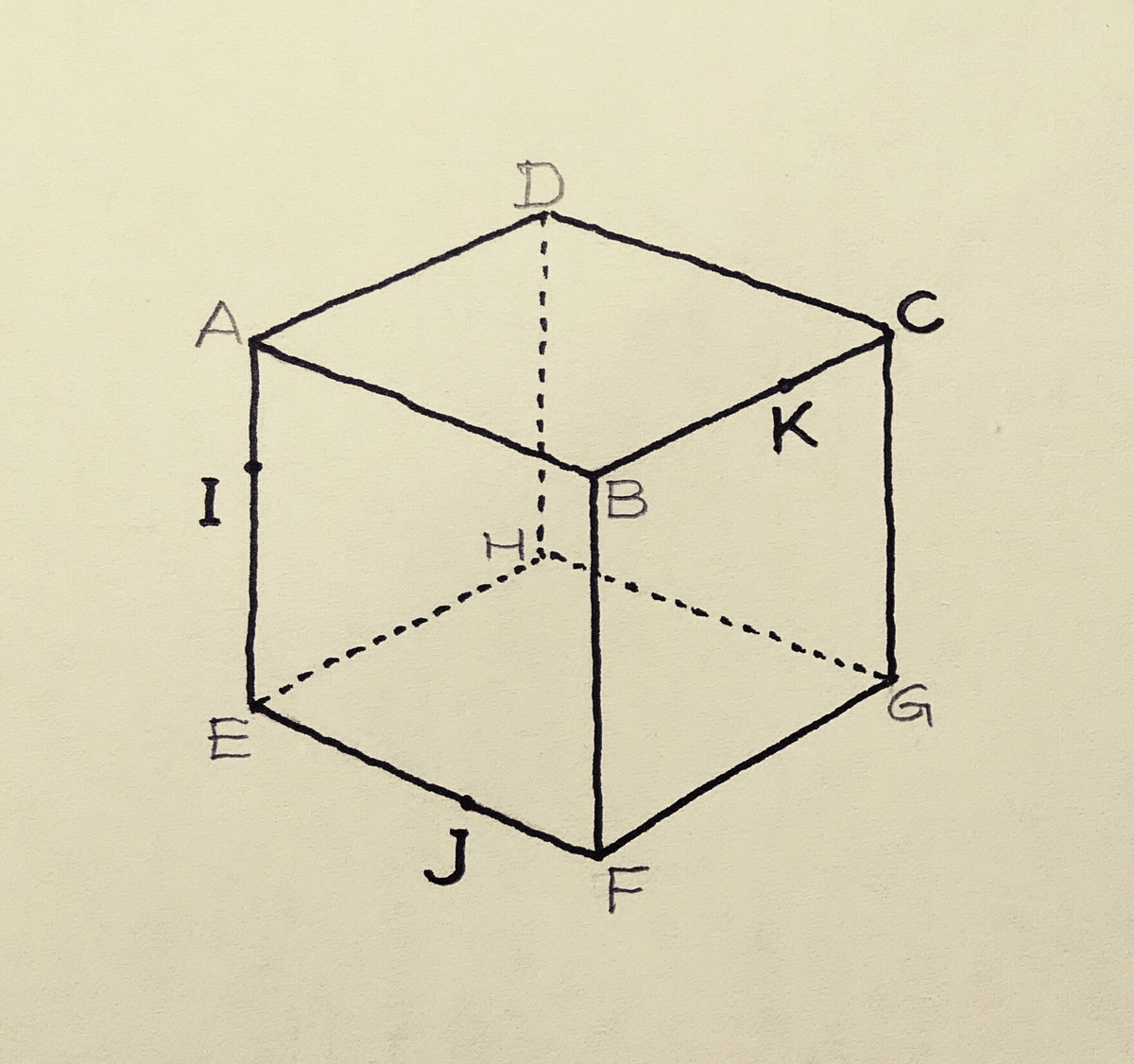
(1)四面体CIJKの体積を求めよ。
(2)3点I,J,Kを通る平面で立方体を切断し、点Bを含む立体を取り除く。
残った立体をさらに3点I,J,Cを通る平面で切断し、点Hを含む立体を取り除く。
最後に残った立体の体積を求めよ。
(答え: 256/3, 496/3)
【解説】
(1)
この四面体は、どの面を底面と考えても、体積を求めにくいですね。
こういう場合は、簡単な立体との
「体積比」
を利用する手法を忘れないようにしましょう。
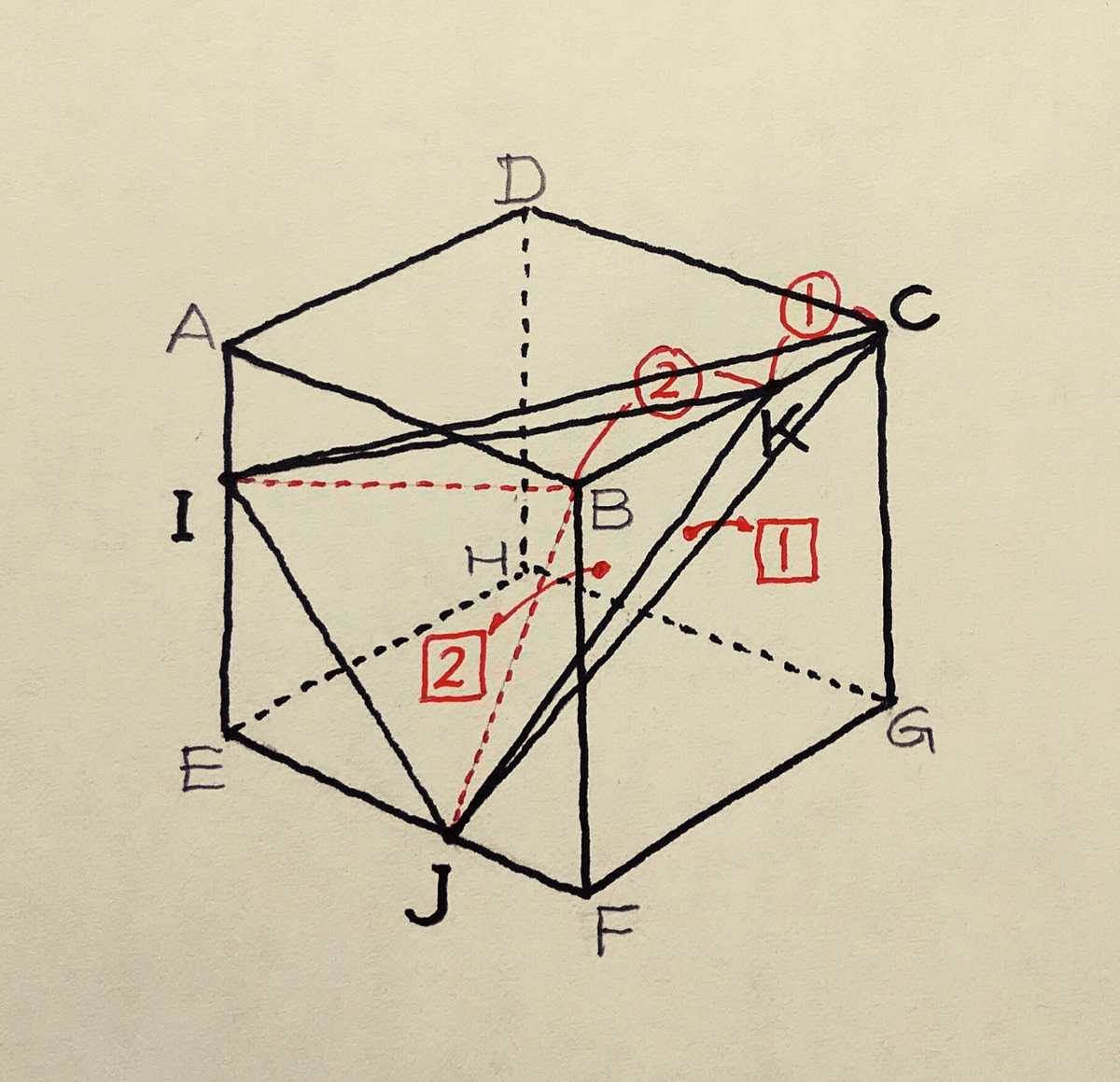
(I-CJK):(I-CJB)
=△CJK:△CJB
=CK:CB
=1:3
∴(I-CJK)=(I-CJB)×1/3=256/3
(I-CJB)ならば、
「底面が△BIJで高さがBCの三角錐」
ですから簡単に体積を求められますね。
(2)
この問題は、「立方体の切断」ができるようになってから臨みましょう。
その上で、(1)を利用すれば簡単に体積を求められることに気づけるようにしましょう。
最後に残った立体は、一発で求めることもできますが、(1)を利用した方が楽ですね。
ですから、まずはこの立体を分割して考えましょう。
すると、
「(1)で求めた四面体」
と、
「四角錐I-CNLK」
と
「四角錐J-COMK」
に分割できますね。
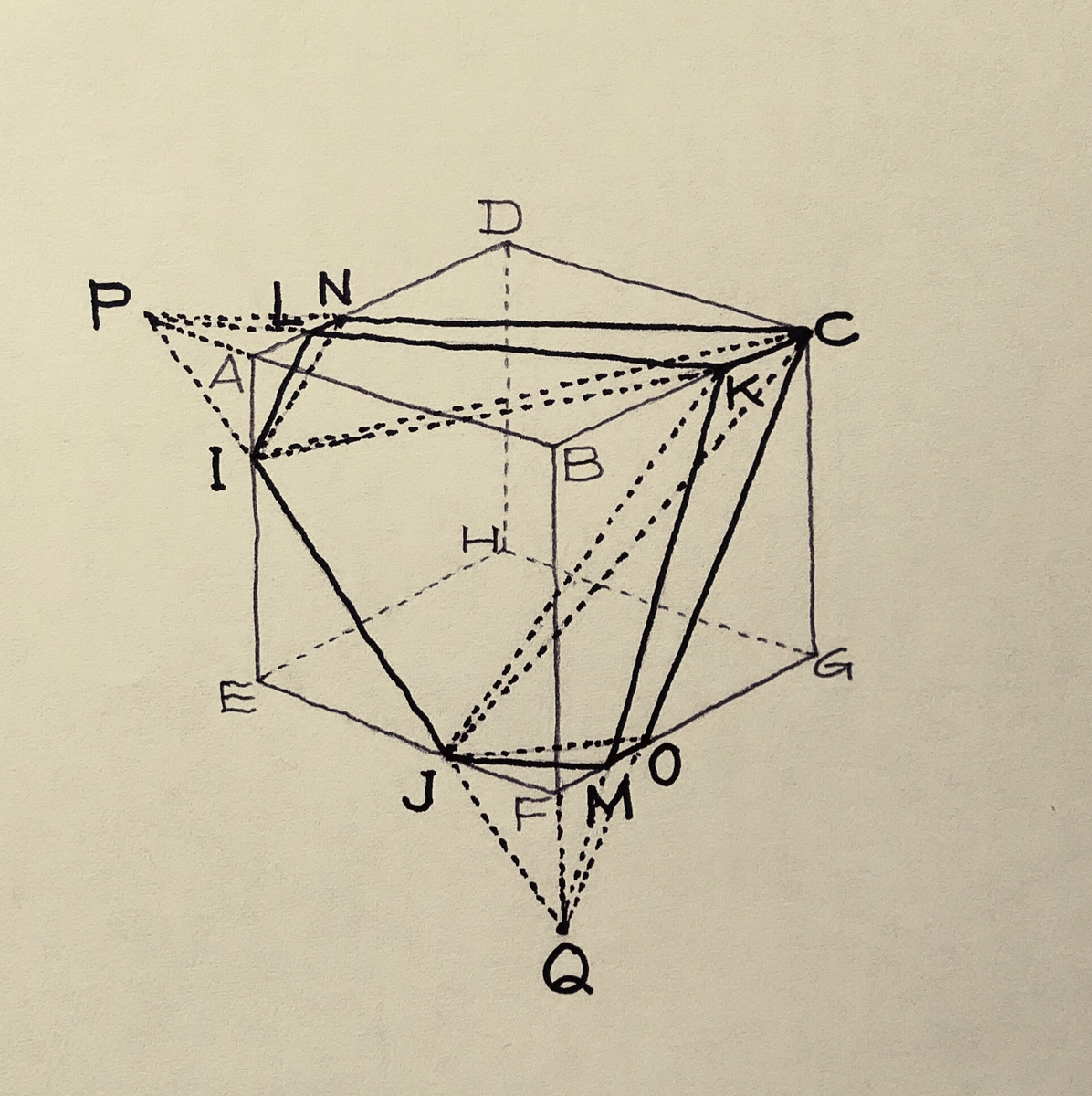
この2つの四角錐の体積は等しく、
(4+1)×12×1/2×4×1/3=40
と簡単に求まりますから、
∴256/3+40×2=496/3
簡単に体積を求められない多面体の場合は、
「体積比の利用」
や、
「分割・除外」
の手法を使えるようにしておきましょう。