正八面体は、その構成をしっかり把握してさえいれば、非常に取り組みやすい立体です。
当初から伝え続けている通り、いかに「正多面体に慣れ親しんできたか」が効いてきます。
例えば、下記のような問題をスラスラ解けるか、チェックしてみましょう。
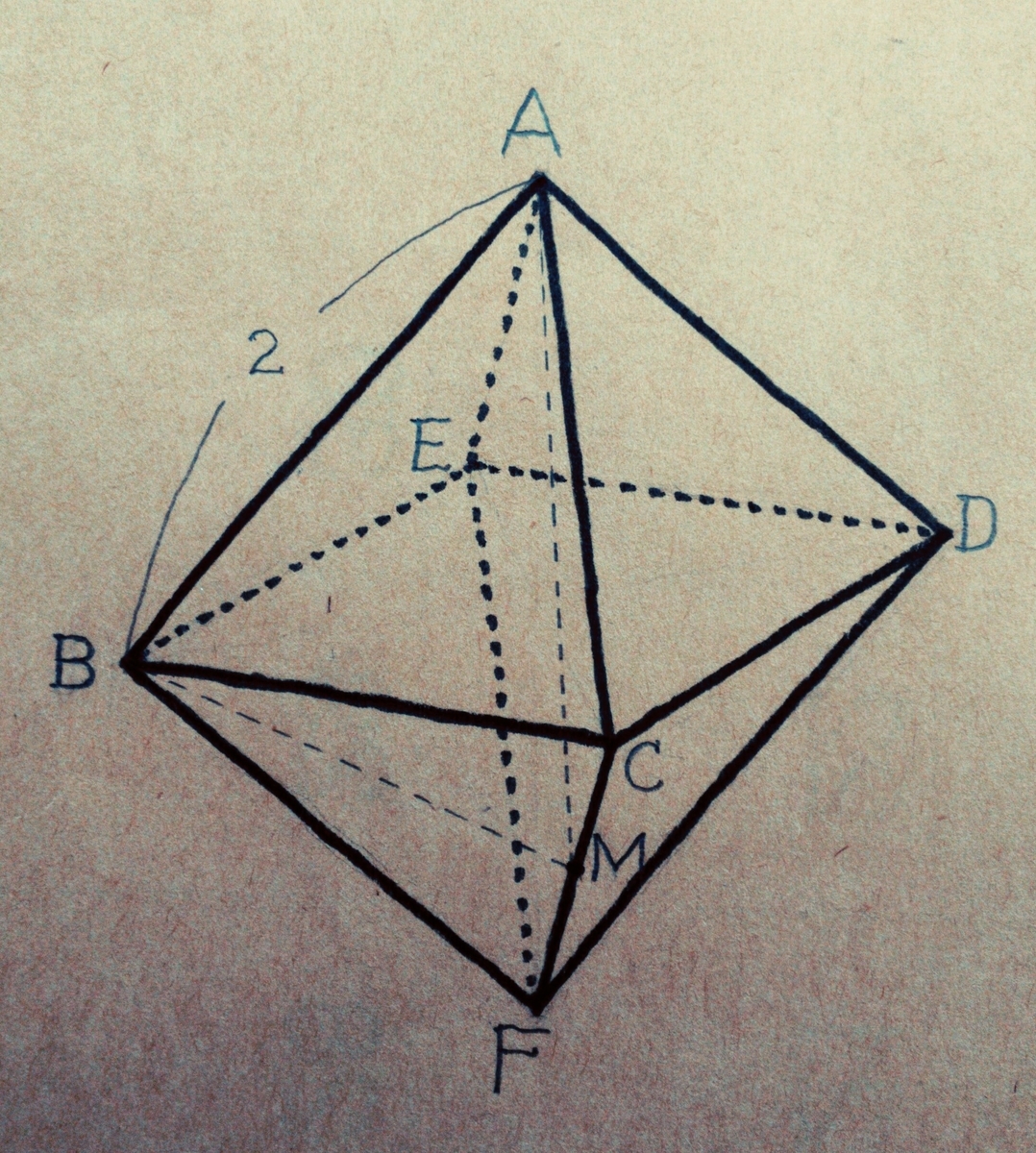
【問題】
1辺の長さが2の正八面体ABCDEF。
Mは辺CFの中点。
(1)この正八面体を「Mを通り面ACDに平行な平面」で切断したとき、切断面の面積は?
(2)△ABMの面積は?
【解答(1)】
まず、
「切断面は正六角形」
ですね。
その1辺は1ですから、
∴√3/4×6=3√3/2
【解答(2)】
△ABMの面積を求めるにあたって犯しやすいミスが、
「高さが平行面間の距離」
と勘違いしてしまうことです。
“三角形の3辺の長さ”がわかるのですから、鉄則通りに攻めるべきです。

まず三平方より
AM=√5,BM=√3
Mから辺ABにおろした垂線の足をH、
AH=xとします。
△AMHと△BMHに着目して三平方より方程式を立てると、
(√5の2乗)-(xの2乗)=(√3の2乗)-{(2-x)の2乗}
これを解いてx=3/2
よってMH=√11/2
∴△ABM=2×√11/2×1/2=√11/2
また、今回は用いませんでしたが、
「正八面体の平行面間の距離」
はすぐ求められるようにしておきましょう。
そうすれば、例えば
「正八面体の内接球(2019桐朋)」
の問題も難なく解けたはずです。
※「正八面体の切断(2020ラ・サール/改題)」
https://mcafejr.hatenablog.com/entry/2020/11/08/171740